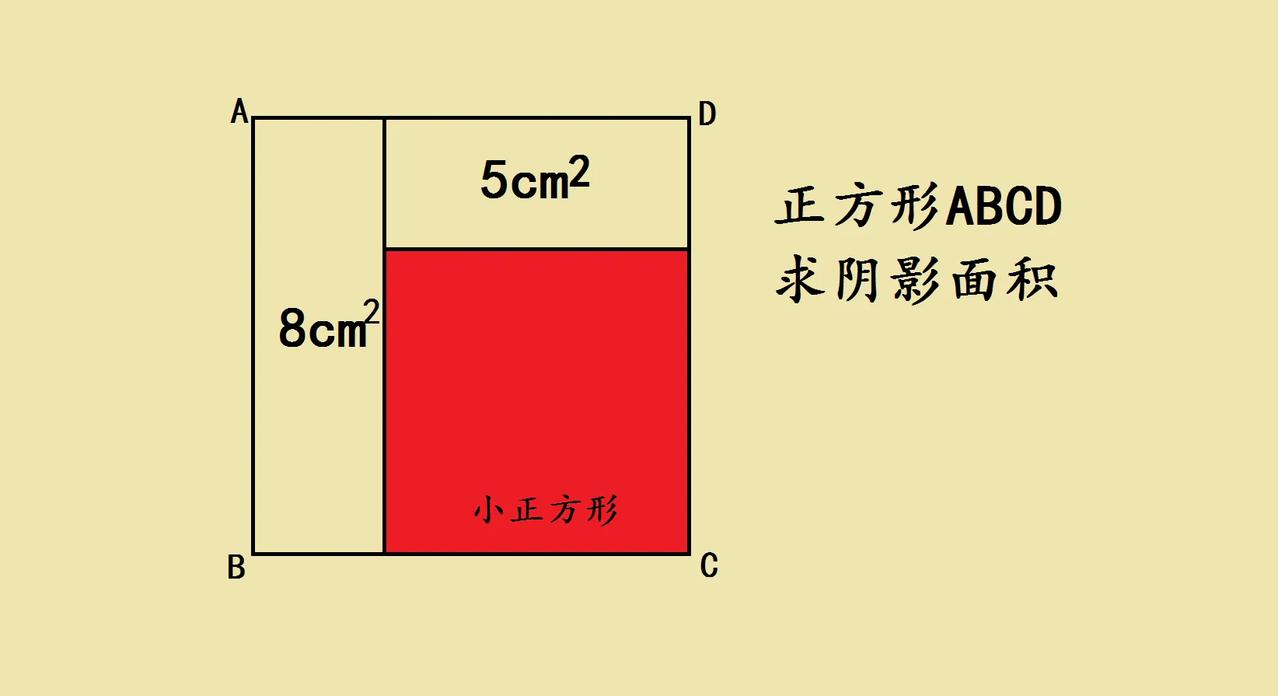
被正方形难住？这题暗藏“面积密码”！ 家人们，今天遇到个超有意思的几何题，盯着图看半天，感觉脑袋里在放“数字烟花”🎆 题目是正方形ABCD，里面有俩长方形，面积分别是8cm²和5cm²，求阴影小正方形的面积。刚开始觉得这怎么算呀，可越琢磨越有门道！ 你看，正方形的边长是统一的，这俩已知面积的长方形，说不定和阴影正方形有“隐藏关系”。想象一下，把它们的边长拆拆看，会不会有相同的线段长度，能通过某种方式让面积相乘或相加，直接关联到阴影面积？ 就像解谜游戏，每个已知面积都是线索，得找到它们和阴影正方形的“连接点”。可能涉及到长方形面积公式（长×宽），以及正方形边长相等的特性，把这些揉在一起，说不定就能解锁答案！ 现在满脑子都是各种边长组合，感觉差一步就能戳破这层窗户纸，这种探索的过程太让人上头啦～有没有几何达人，快来感受下这题的奇妙，一起找找这藏在正方形里的“面积密码”！
评论列表
猜你喜欢
【7评论】【3点赞】
【1评论】【1点赞】
![没想到吧，人家追出国后，又又又回来了[吃瓜][吃瓜]](http://image.uczzd.cn/4217158522888850182.jpg?id=0)
【5评论】【2点赞】
作者最新文章
热门分类
狗皮膏药
25/3
左右
大正方形边长a，小正方形边长b，a²-b²＝13，质数，所以a+b＝13，a-b＝1，a＝7，b＝6。小正方形面积36。
左右 回复 08-19 17:26
所以很可能这个题本身就是错的。
左右 回复 08-19 17:24
用的平方差公式a²-b²＝(a+b)(a-b)＝13，因为13是质数，只有1/13两个因数，所以是13✖️1＝13。我发了解题过程后也发现和楼上的用十字分割法解出的结果有很大差异，具体是什么原因就不清楚了，因为两个方法看起貌似都没问题。
qing9
[5/（8-5）½]²