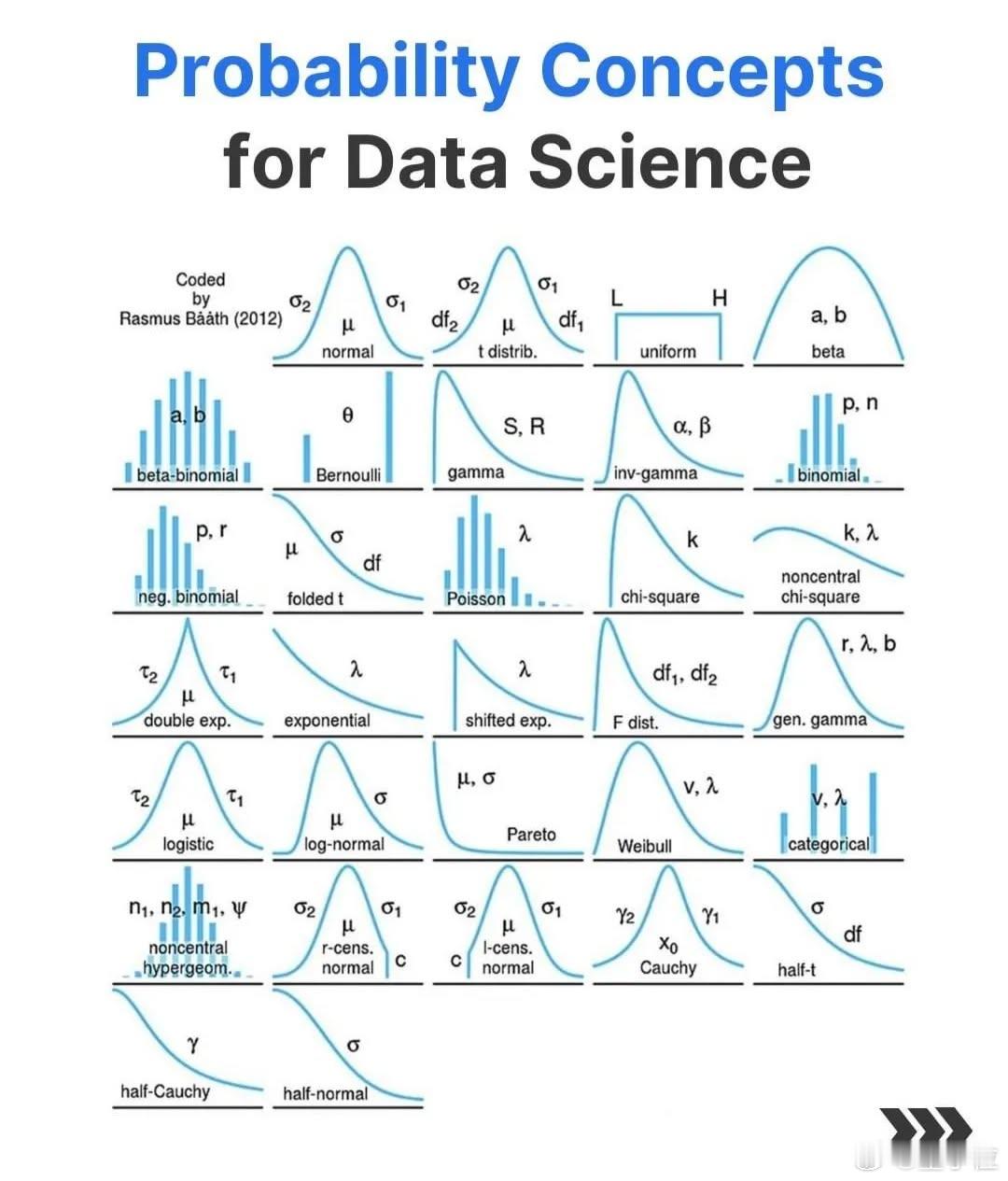
人类已知概率分布图鉴一图看懂各类概率分布
一图囊括人类已知大部分概率分布,建议收藏。
这些概率分布横跨自然现象、人类行为、机器学习、工程建模等各个领域。
下面简单介绍每种分布,按图中排布顺序来:
第一排:经典连续型分布
- Normal(正态分布):大自然最常见的分布,受多个独立因素影响后的结果,比如身高、IQ等。
- t 分布:近似正态,但更“胖尾”,常用于样本较小时的平均值检验。
- Uniform(均匀分布):每个取值概率一样,适合表示“完全未知”的情况。
- Beta 分布:值域在[0,1],可以塑造各种形状,常用于表示概率的分布。
第二排:离散型与偏态分布
- Beta-binomial(β-二项):考虑概率本身不固定的二项分布。
- Bernoulli(伯努利分布):抛一次硬币的结果,只有成功/失败。
- Gamma(伽马分布):偏态分布,用于建模等待时间。
- Inv-Gamma(逆伽马):常用于表示方差的不确定性。
- Binomial(二项分布):重复做n次伯努利试验,统计成功次数。
第三排:偏态与极端分布
- Neg. binomial(负二项分布):试验进行到第r次成功前所需失败次数。
- Folded t:对t分布取绝对值,常用于处理非负变量。
- Poisson(泊松分布):单位时间内事件出现的次数,比如一分钟接到几通电话。
- Chi-square(卡方分布):正态分布变量平方和,用于假设检验。
- Noncentral chi-square(非中心卡方):偏移参数更复杂,假设检验中常出现。
第四排:指数家族
- Double exp(拉普拉斯分布):尖峰重尾版正态分布。
- Exponential(指数分布):建模等待某个事件的时间,比如下一位客户什么时候来。
- Shifted exp:偏移后的指数分布。
- F分布:两个方差的比值,常用于方差分析(ANOVA)。
- General gamma(广义伽马):能变出很多其他分布的“万金油”。
第五排:人类行为建模中常见
- Logistic(逻辑斯蒂分布):类似正态但尾部更肥,常见于分类模型中。
- Log-normal(对数正态):一堆东西乘出来的结果,比如城市人口、股价。
- Pareto(幂律分布):俗称“80/20法则”,比如20%的人赚80%的钱。
- Weibull(威布尔分布):建模寿命、可靠性、设备故障率。
- Categorical(分类分布):多类别之间的离散选择,比如抽卡结果。
第六排:罕见但有用的分布
- Noncentral hypergeometric(非中心超几何):复杂抽样问题用得上。
- Right/Left censored normal:截断正态分布,表示某些数据只能看到一部分。
- Cauchy(柯西分布):极端值极多,均值都不存在,常用于反例。
- Half-t(半t分布):只保留t分布的正半部分。
第七排:半分布
- Half-Cauchy(半柯西):只有正值,常用于建模标准差的先验。
- Half-normal(半正态):去掉负值后的正态分布,常用于建模非负误差。
这张图是由Rasmus Bååth在2012年整理的“分布图谱”,现在依然是初学者、数据分析师、模型工程师理解建模世界的一张基础地图。