[LG]《Policy Learning with Abstention》A Sawarni, J Jin, J Whitehouse, V Syrgkanis [Stanford University] (2025)
策略学习中的弃权机制:安全决策的新框架
在高风险领域如个性化医疗和广告,策略学习算法常用于从观测数据中构建个性化治疗规则。但传统方法的一个关键缺陷是:在预测不确定时仍强制决策,这可能导致严重后果。本文介绍了一种创新框架——策略学习中的弃权(Policy Learning with Abstention),允许算法在不确定区域“弃权”,即推迟到安全默认策略或专家决策,从而提升安全性。
核心问题与框架设计
策略学习的目标是基于观测数据 \( Z = (X, D, Y) \)(协变量 \( X \)、治疗 \( D \in \{0,1\} \)、结果 \( Y \in [0,1] \)),学习一个弃权策略 \( \pi: \mathcal{X} \to \{0,1,*\} \),其中 \( - \) 表示弃权。弃权时,奖励为随机猜测的价值加上小额奖金 \( p \geq 0 \),即 \( \frac{Y(1) + Y(0)}{2} + p \)。这激励算法在条件平均治疗效应(CATE, \( \tau_o(x) = g_o(1,x) - g_o(0,x) \))不确定时弃权,避免盲目决策。
假设包括无混杂(unconfoundedness)和严格重叠(strict overlap, 倾向评分 \( p_o(x) \in [\kappa, 1-\kappa] \))。策略类 \( \Pi \) 具有有限 VC 维 \( d < \infty \)。弃权遗憾定义为 \( \mathrm{Reg}_n^{(p)}(\pi) = V(\pi^*) - V^{(p)}(\pi) \),其中 \( V(\pi^*) \) 是类内最优二元策略价值,\( V^{(p)}(\pi) \) 是弃权价值。奖金 \( p \) 充当“合成边际”,无需标准边际假设即可实现快速收敛。
算法与理论保证
提出两阶段学习器(算法1):首先在数据一半上计算经验福利最大化器 \( \hat{\pi} \),然后构建近最优策略集 \( \hat{\Pi} \)(经验价值接近 \( \hat{\pi} \)),基于与 \( \hat{\pi} \) 的分歧构造弃权类 \( \tilde{\Pi} \),在另一半数据上最大化弃权福利。
- 已知倾向评分:使用逆倾向加权(IPW)去偏。定理3.1证明,在概率 \( 1 - \delta \) 下,弃权遗憾 \( \mathrm{Reg}_n^{(p)}(\tilde{\pi}) \lesssim \frac{d \log(n/d) + \log(1/\delta)}{p n \kappa^2} \)(\( O(1/n) \) 快速率)。当 \( p=0 \) 时,退化为标准 \( O(1/\sqrt{n}) \) 率,与Athey和Wager (2021)匹配(命题3.3)。无需估计CATE,避免复杂函数建模难题。
- 未知倾向评分:使用双重鲁棒(DR)目标,引入伪结果 \( \hat{\varphi}(x,d,y) = \hat{g}(d,x) + \frac{D}{\hat{p}(x)} (y - \hat{g}(d,x)) + \frac{1-D}{1-\hat{p}(x)} (y - \hat{g}(d,x)) \)。定理3.4证明,遗憾上界为 \( \frac{d \log(n/d) + \log(1/\delta)}{p n \kappa^2} + \frac{\mathrm{Err}_{DR}^2}{p \kappa^2} \),其中 \( \mathrm{Err}_{DR} \) 是nuisance产品误差。若 \( \mathrm{Err}_{DR} = o_p(n^{-1/2}) \)(常见于VC类或树模型),则恢复快速率。
这些保证扩展了分类弃权文献(Bousquet和Zhivotovskiy, 2021),处理观测数据的反事实性质。奖金 \( p \) 提供“合成边际”:当 \( |\tau_o(x)| < p \) 时弃权优于任何二元决策;反之,决策更确定。
关键应用:提升策略学习鲁棒性
框架作为黑箱工具,解决多个核心问题,增加理论深度:
1. 无需标准边际假设的快速学习率(定理4.1和4.2):传统快速率需CATE远离零(边际条件 \( \mathbb{P}(|\tau_o(X)| \geq h) = 1 \))和可实现性(Bayes策略在 \( \Pi \) 中)。算法2在第一阶段用 \( p = h/2 \) 弃权,第二阶段在弃权区域精炼(有限组合直径D时用EWM,或CATE预言机)。定理4.1:在有限D下,遗憾 \( \lesssim \frac{D + d \log(n/d) + \log(1/\delta)}{\kappa^2 h n} \)(\( O(1/n) \))。定理4.2:用CATE预言机(L2率 \( n^{-\beta} \)),遗憾分解为三项:\( O(n^{-1}) \)(弃权阶段)、\( O(n^{-2\beta}) \)(类逼近)和混合项,统一了可实现(\( \beta=1/2 \))与回归率保证。即使不可实现,若类逼近小(\( V(\pi^B) - V(\pi^*) = o(1) \)),优于直接分类器。
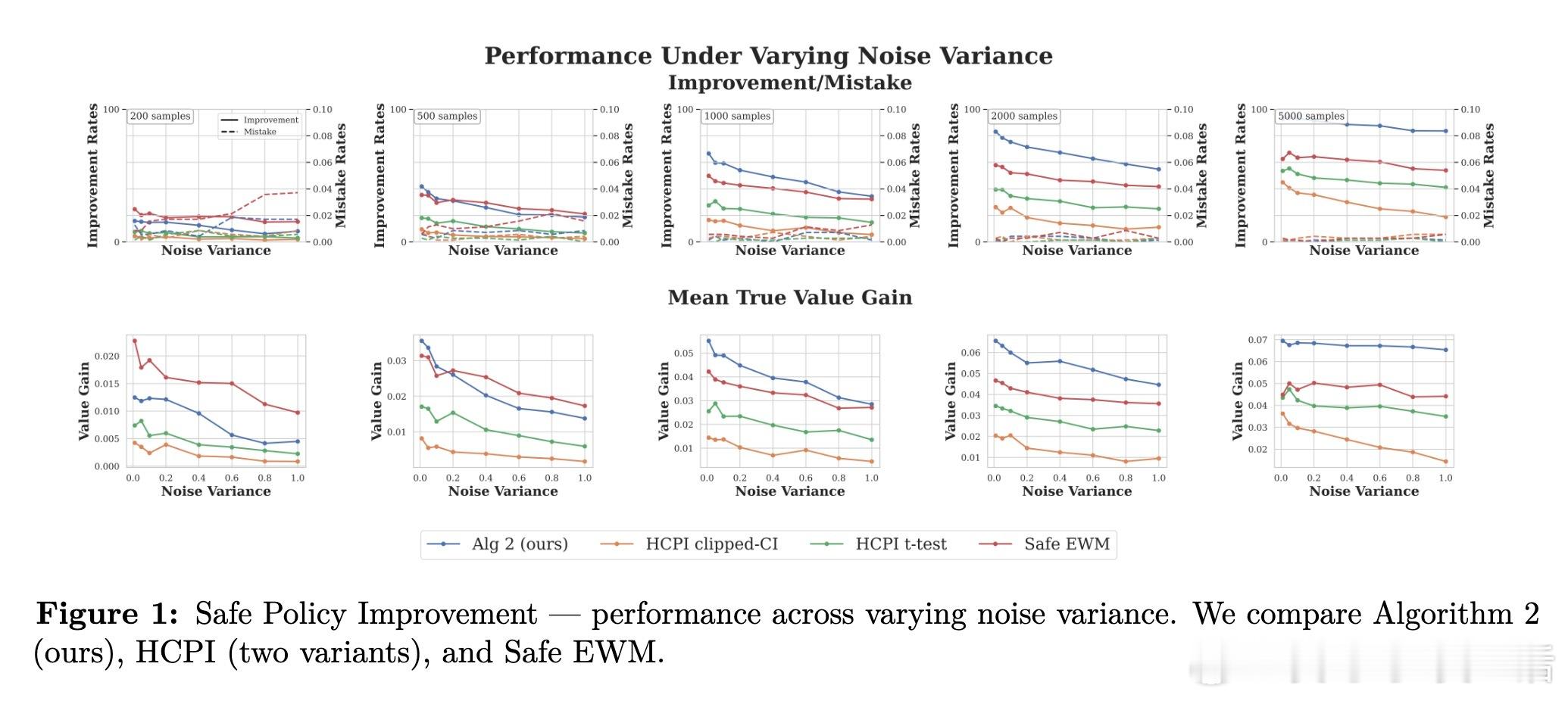
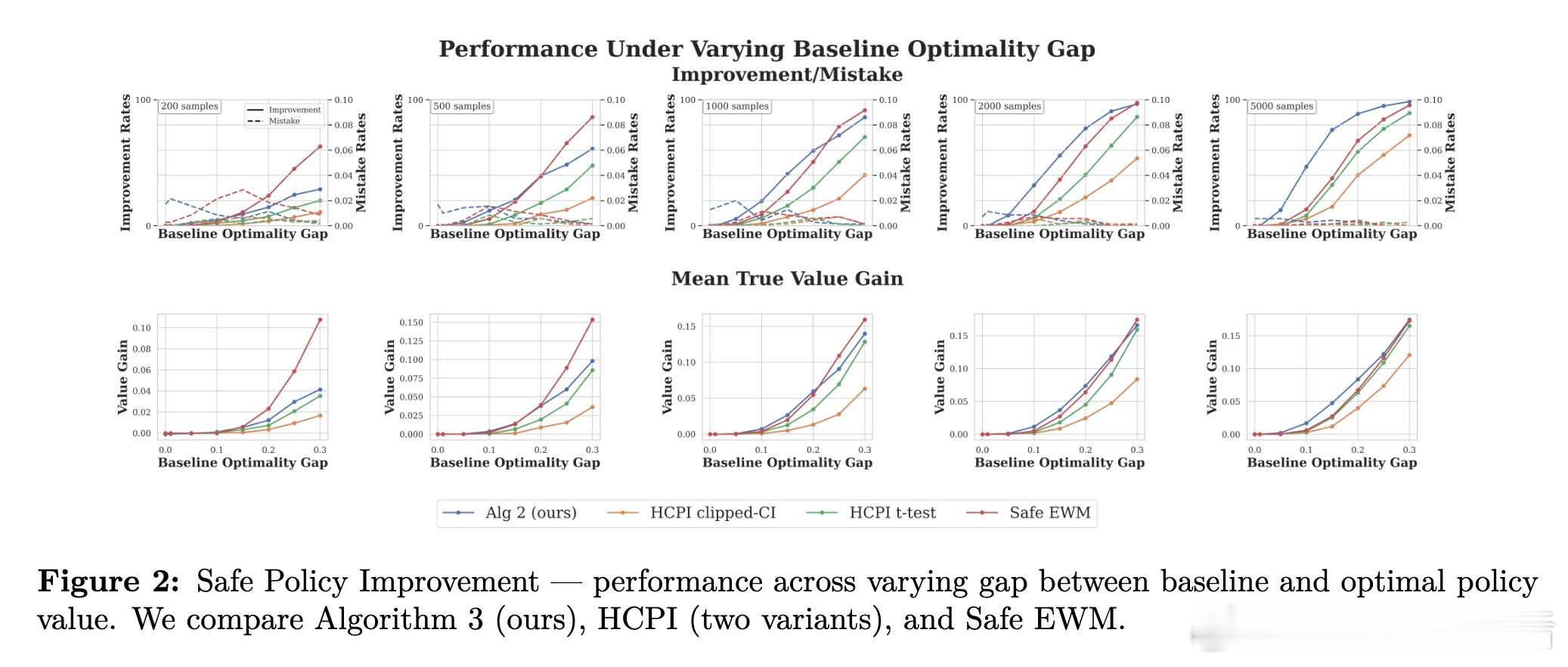
2. 安全策略改进(算法3):目标是高概率优于基线 \( \omega \)。用样本分割(训练/测试),在网格奖金 \( \mathcal{P} \) 上运行算法1,弃权替换为 \( \omega \),测试LCB > 0。实验(图1-2)显示:在噪声方差0.01-1.0和基线-最优差距变化下,算法3在n≥1000时主导:改进率最高、价值增益最大、错误率控制在δ=0.05。优于HCPI (Thomas et al., 2015)和Safe EWM,尤其在小样本外,提供最佳安全-功效权衡。
3. 分布偏移鲁棒性(命题4.3):弃权价值 \( V^{(p)} \) 对结果分布偏移提供对冲。假设真分布在训练分布的W1球(半径α)内,最坏情形价值等价于 \( V^{(\alpha/2)}(\pi) - \alpha \)。随机化(输出1/2,等价弃权)充当对冲:确定策略易受系统偏移影响,而弃权/随机化分散风险。这连接弃权与分布鲁棒学习,奖金 \( p = \alpha/2 \) 自然对齐不确定性惩罚。
思考与启示
弃权框架不仅填补策略学习的安全空白,还揭示弃权作为“多功能工具”的潜力:它模拟边际、确保安全改进,并对冲分布偏移。在高风险场景中,强制决策的“过度自信”可能放大错误;弃权鼓励谦逊,优先证据强度。这启发实际部署:如医疗中,弃权可递交专家;在广告中,避免低置信推送。未来方向包括连续治疗、多臂设置和高效实现(如决策树优化)。实验证实框架实用性,理论保证其统计效率。
总体而言,此工作强调:在不确定性时代,智能“知道何时不知道”比盲目行动更可靠。策略学习应从“全知”转向“安全”范式。
原论文链接:arxiv.org/abs/2510.19672