[LG]《Imbalanced Gradients in RL Post-Training of Multi-Task LLMs》R Wu, A Samanta, A Jain, S Fujimoto... [Meta AI] (2025)
多任务LLM RL后训练中的梯度不平衡问题:一个系统性研究
在大型语言模型(LLM)的多任务学习中,我们常常通过混合不同任务的数据集进行联合优化,以实现跨领域泛化。但这项新研究揭示了一个隐忧:在RL后训练阶段,梯度不平衡现象普遍存在,可能导致优化偏向某些任务,损害整体性能。
1. 问题本质:梯度不平衡的隐形偏置
传统多任务后训练假设所有任务贡献的梯度幅度相似,但现实中并非如此。研究使用Qwen2.5-3B/7B和Llama-3.2-3B模型,在RLVR框架下以GRPO算法训练,考察两种设置:
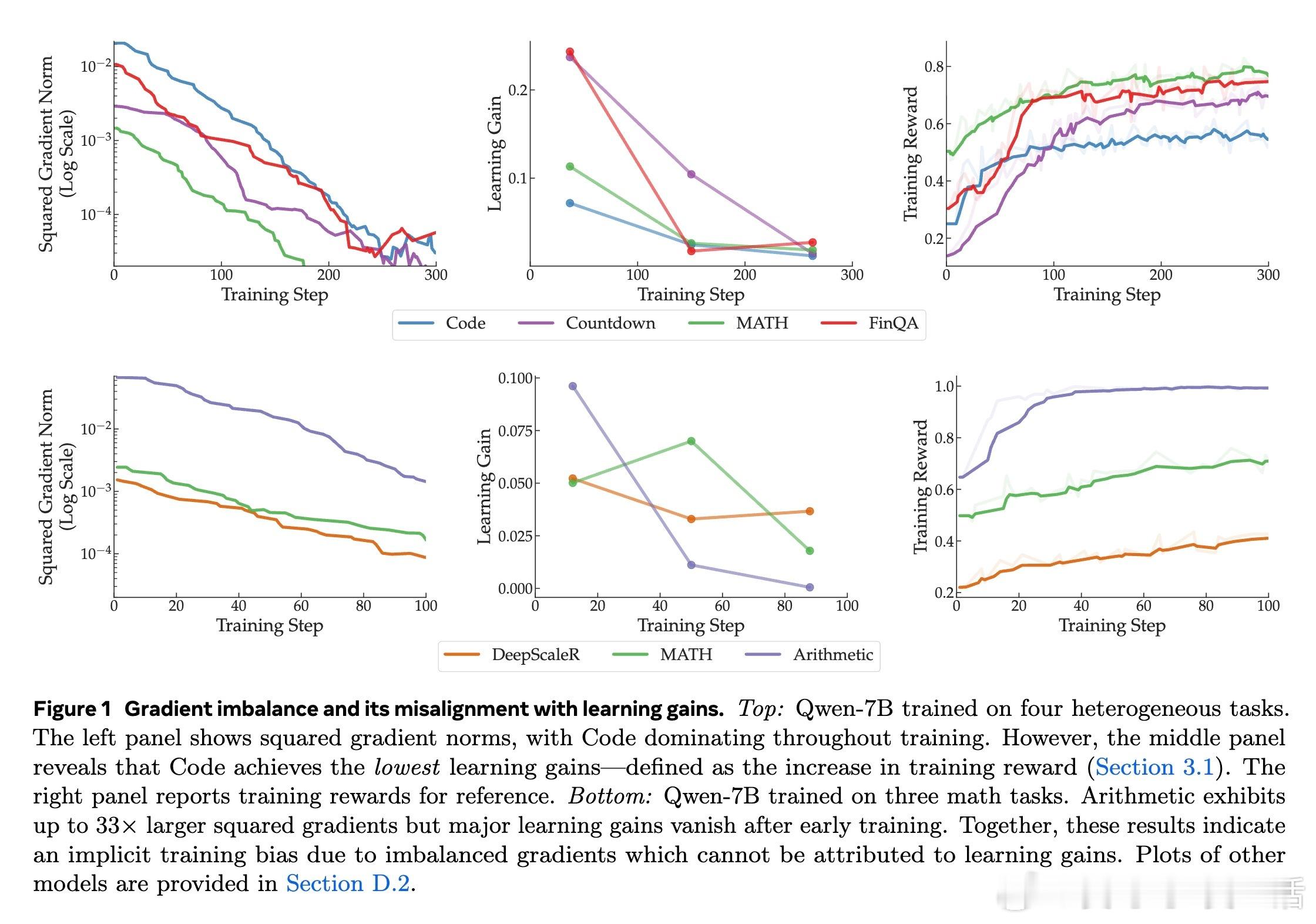
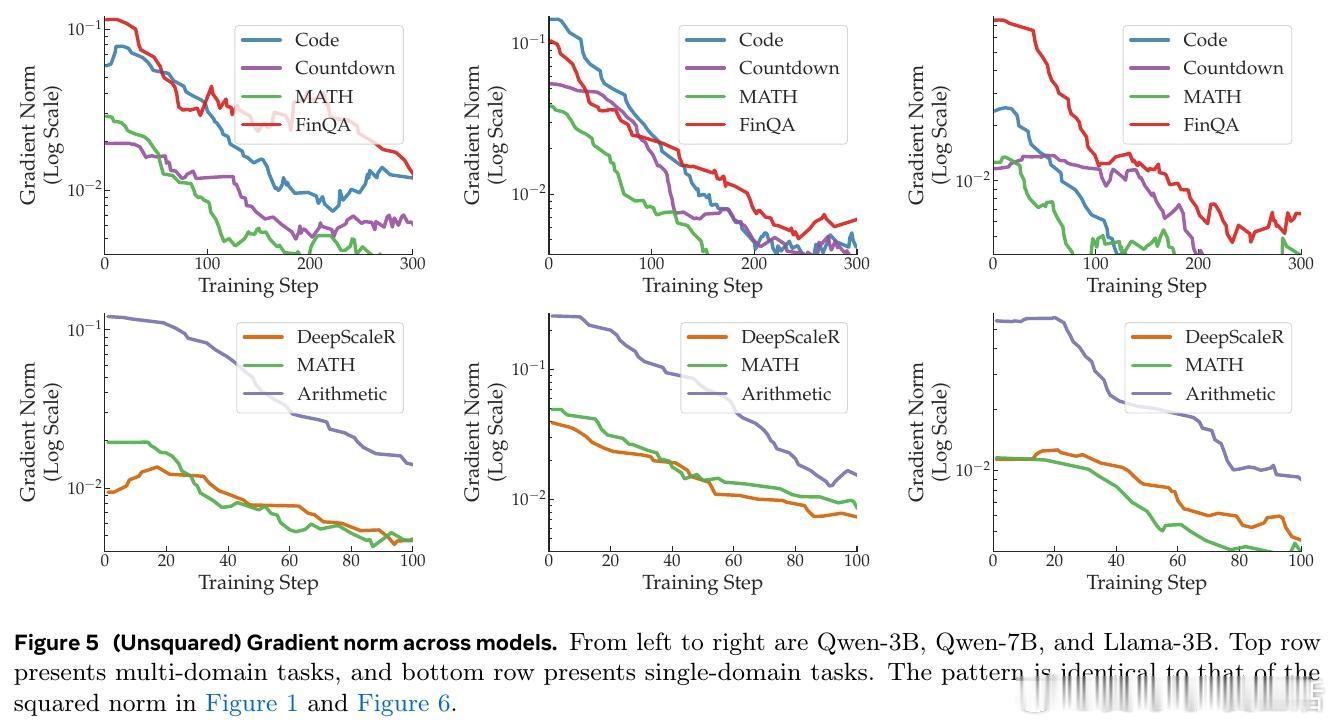
- 多领域任务:包括代码生成(Code)、数字构建(Countdown)、数学问题求解(MATH)和金融推理(FinQA)。结果显示,Code任务的平方梯度范数可达MATH的15倍,主导整个优化过程。
- 单领域(数学)任务:DeepScaleR(高难度数学)、MATH(中等)和Arithmetic(基础算术)。Arithmetic的平方梯度范数高达其他任务的33倍,早起主导但后期衰减。
这种不平衡如何影响训练?梯度平均时,大梯度任务(如Arithmetic)会主导更新,相当于其有效学习率高出5.7倍(√33)。为稳定训练,我们需降低全局学习率,导致小梯度任务(如MATH)被低估。这违背了多任务学习的平等原则,类似于“富者愈富”的优化陷阱。从更深层看,这提醒我们:LLM的多任务训练并非简单叠加数据集,而是需考虑梯度几何的内在异质性。
2. 关键发现:大梯度不等于大收益
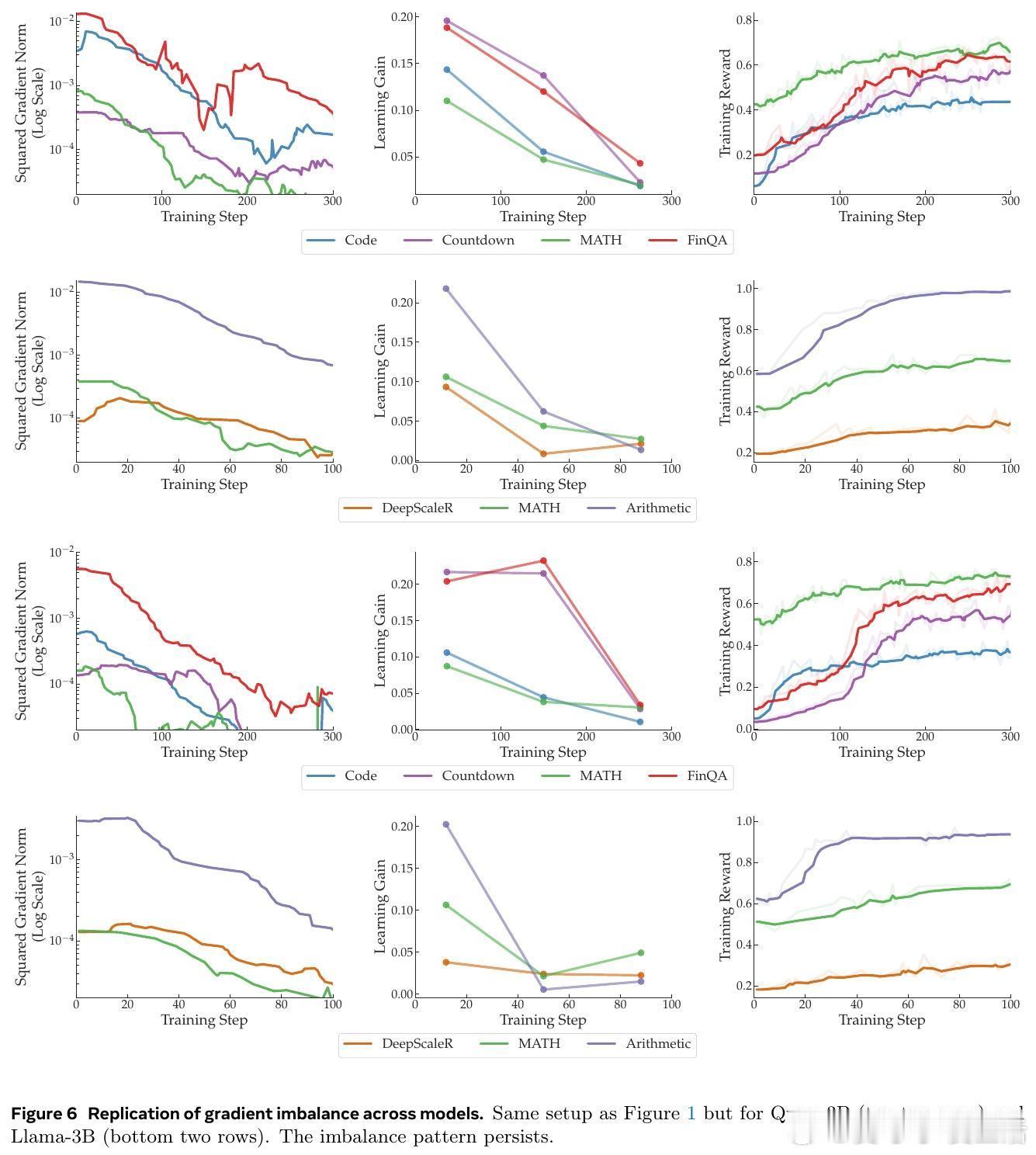
如果大梯度反映更大改进空间(学习收益),不平衡或许合理。但研究通过量化验证推翻了这一假设:
- 学习收益定义:以训练奖励增量衡量(Gain(t) = 未来s步平均奖励 - 过去s步平均奖励)。在多领域中,Code梯度最大,却收益最低;单领域中,Arithmetic早起收益高但后期为零,而小梯度任务持续改进。
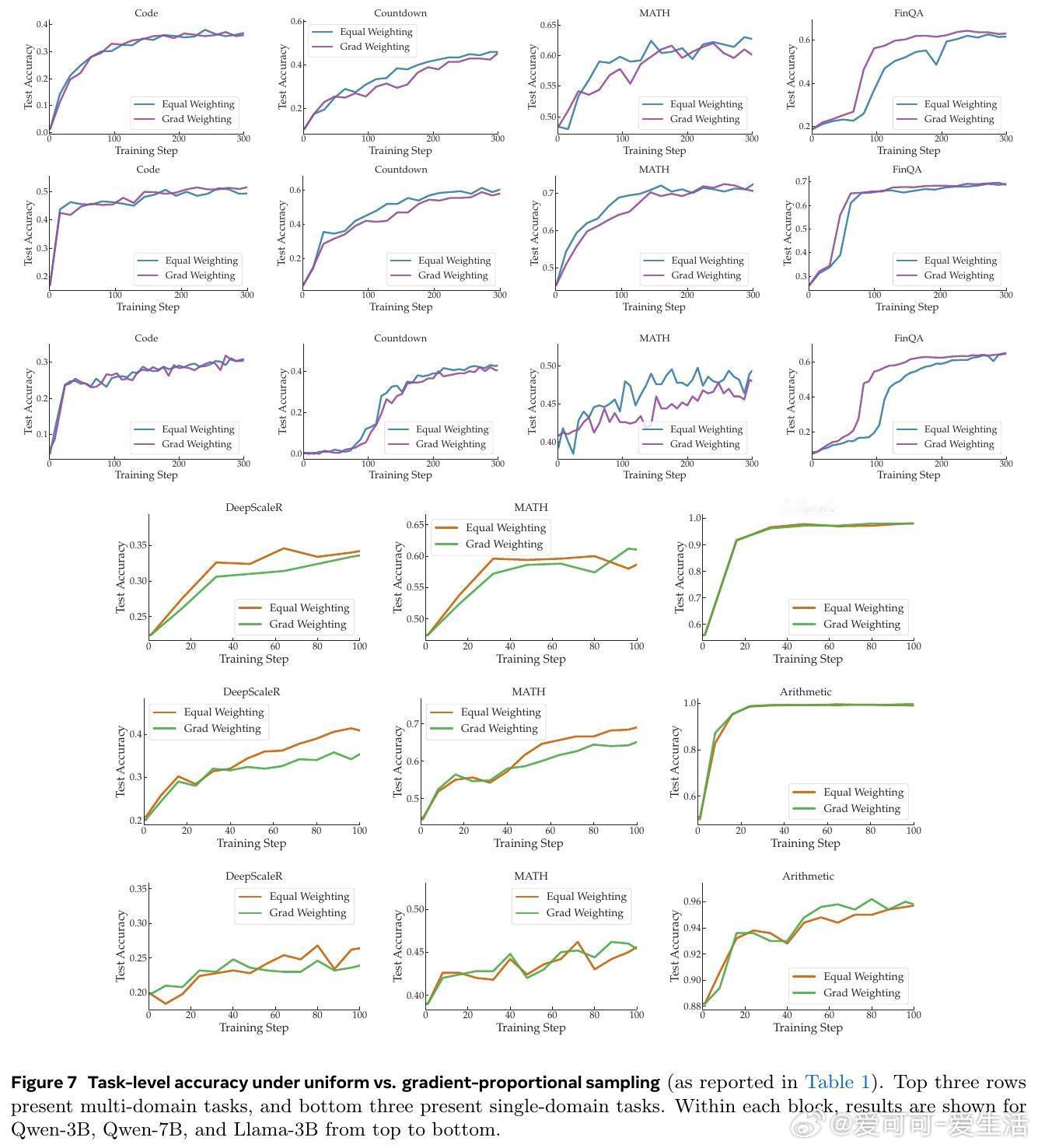
- 梯度比例采样实验:不是均匀采样,而是按梯度幅度softmax采样(最低10%概率避免卡住)。结果:在Table 1中,Qwen-7B多领域平均准确率从61.97%降至60.48%;单领域从69.67%降至66.00%。大梯度任务(如FinQA、Arithmetic)准确率略升,但整体平均下降,证明优先大梯度会牺牲小梯度任务,误导训练。
我的思考:这挑战了机器学习中常见的“梯度幅度代理收益”直觉(如Settles et al., 2007)。理论上(凸分析视角),单任务内平方梯度范数与次优差距成比例(光滑性和PL条件),学习收益可近似此差距。但跨任务时,光滑参数β和PL常数µ异质,导致不匹配。这启发我们:未来可通过任务特定归一化(如自适应β估计)修正梯度,实现更公平优化。
3. 成因探析:非典型统计所能解释
研究检查常见训练统计,均无法解释不平衡:
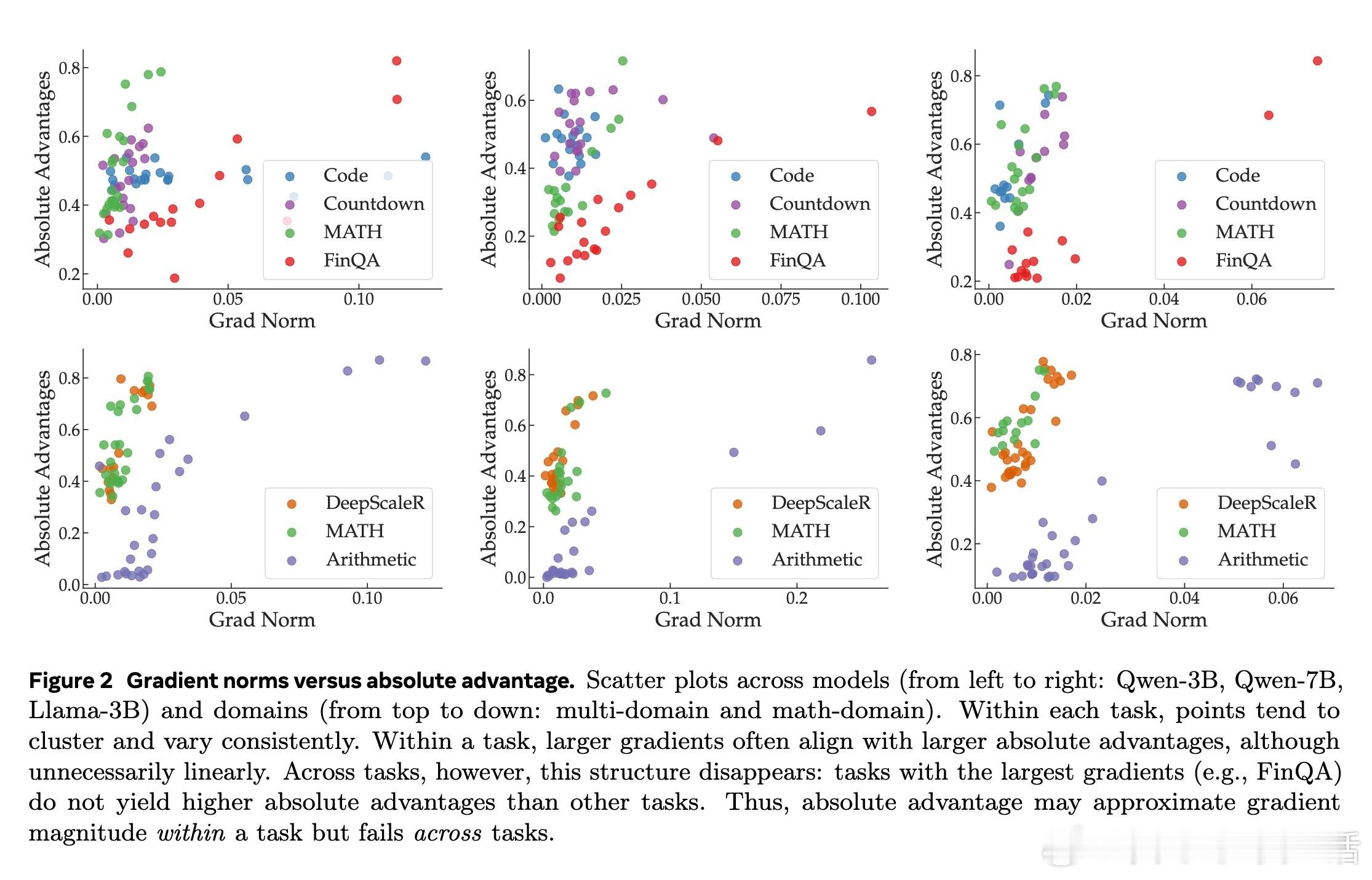
- 优势函数(Advantage):政策梯度定理暗示|A|近似梯度幅度(Jensen不等式)。散点图(Figure 2)显示,单任务内正相关,但跨任务失效——同等|A|下,FinQA梯度远大于MATH。
- 训练奖励/难度:易任务(如高准确率)不一定大梯度;极端0%或100%准确率时,优势趋零,梯度也小。无跨任务模式。
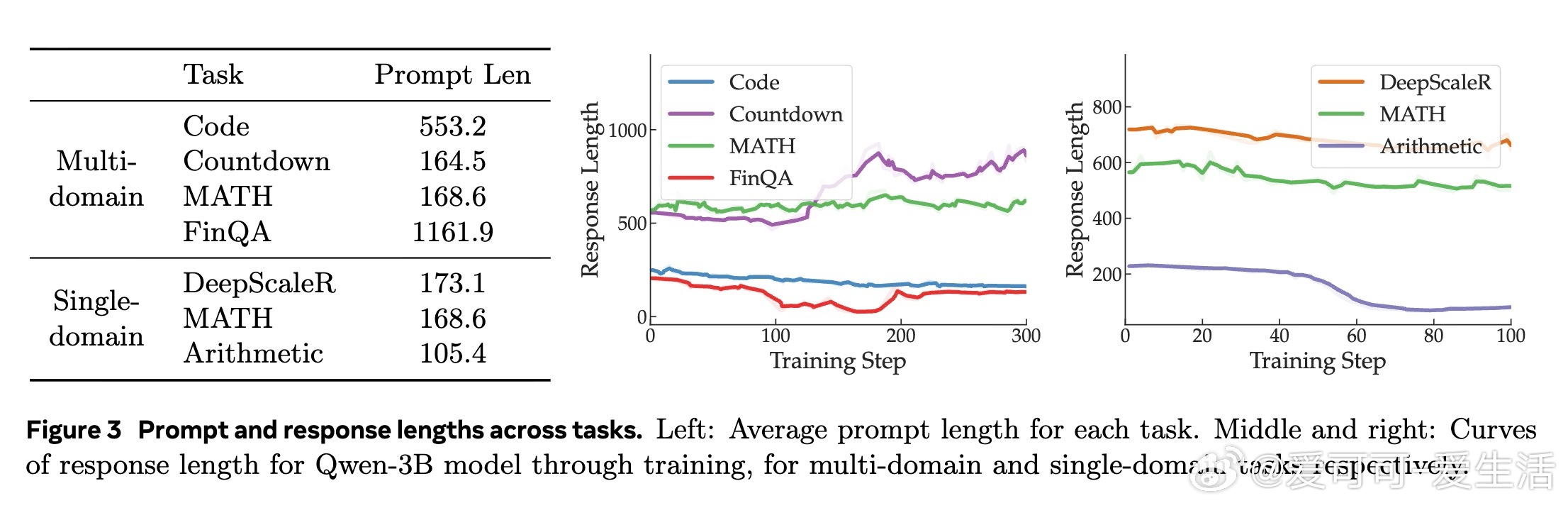
- 序列长度:提示/响应长度差异大(FinQA提示长达1161 token),但政策梯度按token平均,本应无关。实证上,短提示Arithmetic梯度最大,反驳此假设。
结论:不平衡源于任务固有差异(如领域异质性或问题风格),而非表面统计。这强调:简单混合数据集风险高,需警惕LLM训练的“黑箱”动态。
4. 启示与展望:迈向均衡优化
这项首创研究警示RL后训练的梯度偏置,可能泛化到预训练或监督微调阶段。未来方向包括:
- 梯度级修正:借鉴优化文献(如Sener & Koltun, 2018),引入任务权重或投影,使梯度可比。
- 几何重构:镜面下降RL(Kakade, 2001)变换梯度表示,缓解异质性。
- 更广验证:扩展到SFT或更大模型,探索伦理影响(如偏置放大)。
总之,这个发现推动LLM多任务训练从“经验驱动”向“原理导向”转型。简单混合已不足以应对复杂性,我们需设计智能机制,确保每个任务公平发声。
原文详见:arxiv.org/abs/2510.19178